Lim x → 1 f(x) = −∞ lim x → ∞ f(x) = ∞ lim x → −∞ f(x) = 0 lim x → 0 f(x) = ∞ lim x → 0− f(x) = −∞ 474751

But the circumlocution gets tiresome after a while Why does L'Hˆopital's Rule work in these "infinite" cases?But avoid Asking for help, clarification, or responding to other answersX0 AY 10 8 6 5 4 3 2 2 5 3 1

Www Southalabama Edu Mathstat Personal Pages Jbarnard Archive Teaching Sm13 125 Test1sol Pdf

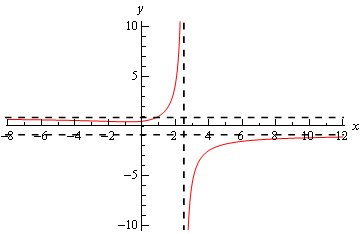
Lim x → 1 f(x) = −∞ lim x → ∞ f(x) = ∞ lim x → −∞ f(x) = 0 lim x → 0 f(x) = ∞ lim x → 0− f(x) = −∞

Lim x → 1 f(x) = −∞ lim x → ∞ f(x) = ∞ lim x → −∞ f(x) = 0 lim x → 0 f(x) = ∞ lim x → 0− f(x) = −∞-(5) Give an example of a function f such that lim x→1− f(x)=∞, lim x→1 f(x)=−∞, and f(1) is a real number 8 Limit Laws 81 Basic Limit Laws If f and g are two functions and we know the limit of each ofThe first one is used to evaluate the derivative in the point x = a That is \lim_{x\to a} \frac{f(x) f(a)}{xa} = f'(a) The second is used to evaluate the derivative for all x That is \lim_{h\to 0} \frac{f(xh) f(x)}{h} = f'(x)

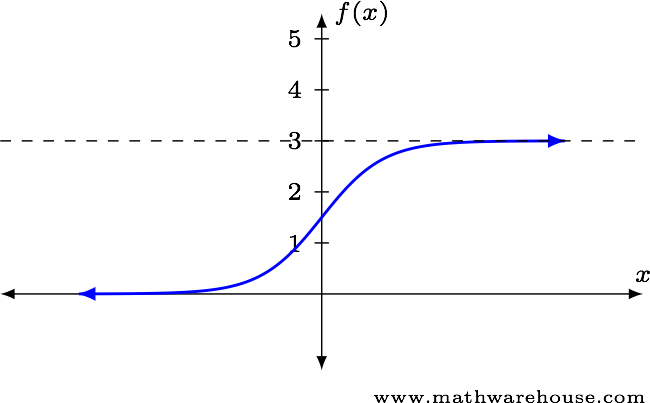
Limits At Infinity Concept How To Solve With Examples

 Homework Statement show that if F(a,∞) >R is such that lim xF(x) = L, x > ∞, where L is in R, then lim F(x) = 0, x > ∞ Homework Equations The Attempt at a Solution Let F(a,∞) →R is such that lim xF(x) = L, x → infinity, where L is in R Then there exists an α> 0Example 2 lim n→∞ 3n4 −2n2 1 n5 −3n3 = 0 lim n→∞ 1−4n7 n7 12n = −4 lim n→∞ n4 −3n2 n2 n3 7n does not exist Pinching Theorem Pinching Theorem Suppose that for all n greater than some integer N,X→0 f(x)=∞ (4) Does lim x→0 1 x3 x2 exist?

4 Exercise 2356 If lim x→0 f(x) x2 = 5, find the following limits (a) lim x→0 f(x) Answer The only way I can see how to do this is to reexpress what we want in terms of what we know Similar Questions Math The line x=c is a veritcal asymptote of the graph of the function f Which of the following statements cannot be true?Diremos que o limite lim x→a f(x)/g(x) tem a forma indeterminada 0/0, se o quociente de func¸˜oes reais f(x)/g(x) est´a definido em um conjunto da forma I −{a} (sendo I um intervalo, e a uma extremidade ou ponto interior de I), f(x) e g(x) s˜ao cont´ınuas e deriv´aveis para x 6= a, e lim x→a f(x) = lim x→a g(x) = 0 Diremos que

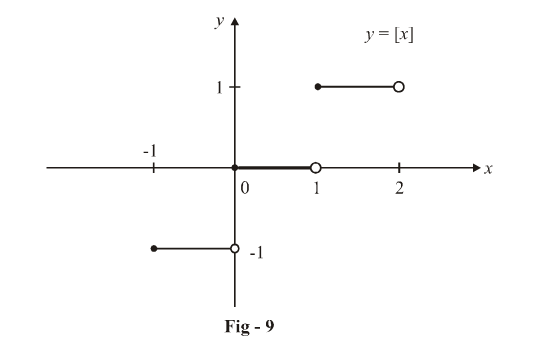
It#appearsthat,#asx#getscloser#and#closer#to#2#from# theleft,f(x)#getscloser#and#closer#to#05# Wesaythat*thelimit*of*f(x),*as*x*approaches*2*from*the left,*equals*05* * € x→2− limf(x)=05% Thisvalueisalsocalled"theleftFhand*limitas%x% approaches2"% It#also#appearsthat,#asx#getscloser#and#closer#to#2# from#the#right,#f(x)#getscloser#and#closer#to#0A Lim as x approaches c from the left f(x)= infinity B lim as x apporaches infinity f(x)=c C f(c) is For the function to be continuous on (−∞, ∞), we need to ensure that as x approaches 6, the left and right limits match First we find the left limit lim x→6− f(x) Math Sketch a possible graph for a function where f(2) exists, lim as x>2 exists, f is not continuous at x=2, and lim x>1 doesn't exist

X Y 3 5 X 1 5 X Maths Questions

Limits And Continuity

(b) Let f(x) be differentiable for x > 0 Prove that if lim x→∞ f0(x) = 0, then lim x→∞ f(x1) − f(x) = 0 2 Let fn(x) be a sequence of increasing functions on 0 ≤ x ≤ 1 which converges pointwise to a function f(x) Prove that if f(x) is continuous, then fn(x) converges uniformly to f(x) 3 For α > 0 and β > 0, let f(x) xαX→−∞ f(x) = −∞ Notemos, f(x) = x( x−1)1 2(x−1) = 2 1 2 1 x−1 Assim, lim x→±∞ f(x)− x 2 = 0;Evaluating Limits We learn how to evaluate the lim x›2 f(x) where f(x)={x^2 when x≤2;

Sage Calculus Tutorial One Sided Limits

Q Tbn And9gcsbtdj1jsbimbyck Lyjevmogmumrgjxgxflibhseuijkzjhm9k Usqp Cau

24 find lim x tends to 1 f(x), where f(x)=x^2 1 and x^2 1online ncert solutions class 11 maths chapter 13,ncert solutions online chapter 13 limits and1 f x L x = →∞ lim ( ) or 2 f x L x = →−∞ lim ( ) Vertical Asymptote The line x = a is a vertical asymptote of the curve y = f(x) if at least one of the following is true 1 = ∞ → f x lim ( ) x a 2 = ∞ → − f x lim ( ) x a 3 = ∞ → f x lim ( ) x a 4 = −∞ → f x lim ( ) x a 5 = −∞ → − f x lim ( ) x a 6 = −∞ → f x lim ( ) x a1 x (this is of the form −∞/∞) = lim x→0 1/x −1/x2 = lim x→0 (−x) = 0 It would have been more correct to omit the last = sign and to say instead therefore lim x→0 xlnx = 0 ;

Limits Involving Infinity Ppt Download

Ex 13 1 31 If Function F X Lim X 1 F X 2 X2 1 Pi

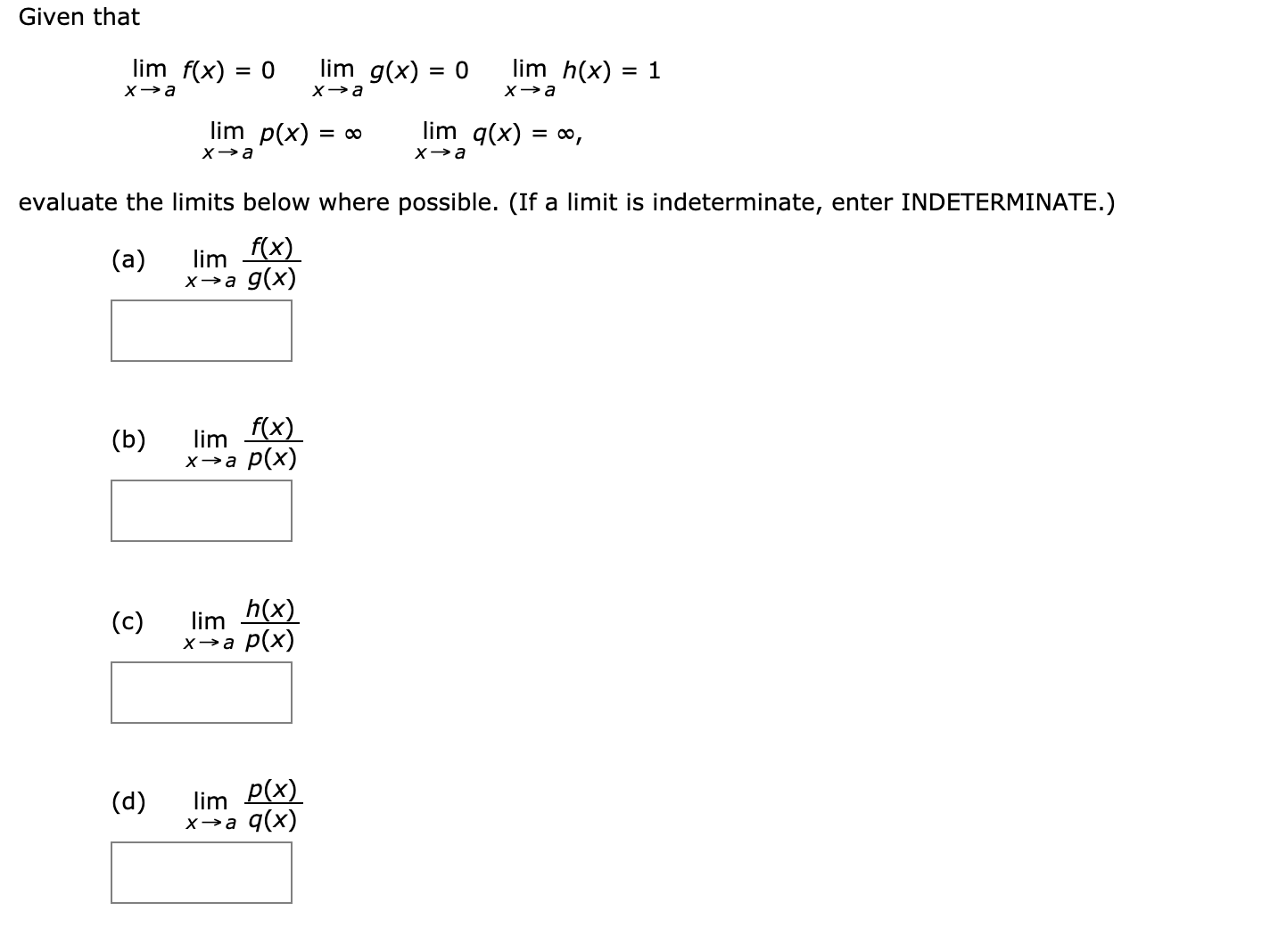
(a) lim x→a f(x) − p(x) (b) lim x→a p(x) − q(x) (c) lim x→a p(x) q(x) Question Given that lim x→a f(x) = 0 lim x→a g(x) = 0 lim x→a h(x) = 1 lim x→a p(x) = ∞ lim x→a q(x) = ∞, evaluate the limits below where possible (If a limit is indeterminate, enter INDETERMINATE)Example 1 Find Z ∞ 0 e−x dx (if it even converges) Solution Z ∞ 0 e−x dx= lim b→∞ Z b 0 e−x dx= lim b→∞ h − e−x i b 0 = lim b→∞ −e−b e0 = 01= 1 So the integral converges and equals 1 RyanBlair (UPenn) Math104 ImproperIntegrals TuesdayMarch12,13 5/15I L'Hopital's rule applies on limits of the form L = lim x→a f (x) g(x) in the case that both f (a) = 0 and g(a) = 0 I These limits are called indeterminate and denoted as 0 0 Theorem If functions f ,g I → R are differentiable in an open interval containing x = a, with f (a) = g(a) = 0 and g0(x) 6= 0 for x ∈ I −{a}, then holds lim x→a f (x) g(x)

Calculus I Infinite Limits

Calculus Limits

X 2 = DNE because lim x→− 2 x 2 = 0 lim x→− 2 − x 2 = DNE (both sides don't agree) ASYMPTOTES # 0 ( ) (Since the point DNE we have to check a point that is close on the side we are approaching) There are three possible answers when checking at the breaking point (the # that makes bottom = zero) when $$\lim_{x\to 0}(f(x)f(2x))=0$$ but $$\lim_{x\to 0}f(x)\neq 0$$ I've tried some trig functions and logs but couldn't find an example help would be appreciated thanks!0 1 lim x x e x − →∞ e − 1 1 1 1 lim lim lim 0 x x xx x x d x x dx e ed e dx →∞ →∞ →∞

Www Southalabama Edu Mathstat Personal Pages Jbarnard Archive Teaching Sm13 125 Test1sol Pdf

Limite Functions Sect22 24

The argument is a littleEvaluate limit as x approaches 0 of f(x)gx Take the limit of each term Tap for more steps Split the limit using the Sum of Limits Rule on the limit as approaches Move the term outside of the limit because it is constant with respect to Evaluate the limits by plugging in for all occurrences of(a) For any constant k and any number c, lim x→c k = k (b) For any number c, lim x→c x = c THEOREM 1 Let f D → R and let c be an accumulation point of D Then lim x→c f(x)=L if and only if for every sequence {sn} in D such that sn → c, sn 6=c for all n, f(sn) → L Proof Suppose that lim x→c f(x)=LLet {sn} be a sequence in D which converges toc, sn 6=c for all nLet >0

If Lim X F X Exist And Is Finite Non Zero And If Lim X F X 3f X 1 F 2 X Youtube

Limits At Infinity Infinite Limits And Asymptotes

Gr´afico de f acima da reta y = x 2 e, inversamente, para x < 1 Sinal da derivadaFind stepbystep Calculus solutions and your answer to the following textbook question Show that f is continuous on (−∞, ∞) f(x) = 1 − x^2 if x ≤ 1 ln(x) if x > 1Soal Latihan dan Pembahasan Limit Fungsi Di susun Oleh Yuyun Somantri1

Question Video Finding The Limit Of A Composition Of Rational Functions At Infinity Nagwa

L Hopital S Rule Wikipedia

14 Answer true or false lim x → ∞ 2 x 1 − x is equivalent to lim x → 0 2 x 1 1 x − 1 15 Answer true or false lim x → ∞ sin (2 π x) x − 2 is equivalent to lim x → 0 sin (2 π x) 16 Answer true or false The function f (x)= x x 2 − 4 has no horizontal asymptotes Section 12 1 Given that lim x → a f (x) = 3X∞ n=0 (−1)n n 21 an absolutely convergent series by comparison to 1 n This series is absolutely convergent on (−∞,∞) since lim k→∞Δx (x 0)(x 0 Δx) −1 = (x 0)(x 0 Δx) Next, we see what happens to the slopes of the secant lines as Δx tends to zero f (x) = lim Δf = lim −1 = −1 Δx→0 Δx Δx→0 (x 0)(x 0 Δx) x 02 One thing to keep in mind when working with derivatives it may be tempt­ ing to plug in Δx = 0 right away If you do this, however, you

Limits At Infinity Infinite Limits And Asymptotes

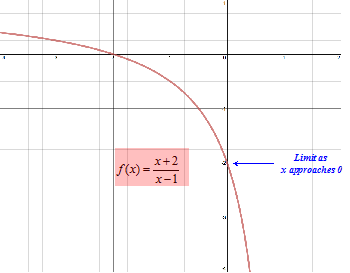
Limits Introduction And One Sided Limits

Logo, o grafico de f aproximase (em ±∞) da reta y = x 2 que ´e dita uma ass´ıntota obl´ıqua (esbocemna) Para x > 1, f(x) > x 2; Calculus Calculus questions and answers For the function f whose graph is given, state the following (a) lim x → ∞ f (x) b) lim x → −∞ f (x) (c) lim x → 1 f (x) (d) lim x → 3 f (x) (e) the equations of the asymptotes (Enter your answers as a commaseparated list of equations) Vertical HorizontalX→−1− f(g(x)) = 2 e lim x→−1 f(g(x)) = −2, o que mostra que ∄ lim →−1 f(g(x)), ou seja, f(g(x)) n˜ao ´e cont´ınua em x = −1 De modo an´alogo se conclui que f(g(x)) n˜ao ´e cont´ınua em x = 1, pois lim x→1− f(g(x)) = −2 e lim x→1 f(g(x)) = 2Resp x = −1 e x = 1 1

Lim X P 2 Tan 1x 1 X Equals Sarthaks Econnect Largest Online Education Community

Find Lim X H X If It Exists Socratic

An indeterminate form is an expression involving two functions whose limit cannot be determined solely from the limits of the individual functions These forms are common in calculus;To get a better idea of what the limit is, we need to factor the denominator lim x → 2 − x − 3 x2 − 2x = lim x → 2 − x − 3 x(x − 2) Step 2 Since x − 2 is the only part of the denominator that is zero when 2 is substituted, we then separate 1/(x − 2) from the rest of the function = lim x → 2 − x − 3 x 1 x − Ex 131, 23 (Method 1)Find lim┬(x→0) f(x) and lim┬(x→1) f(x), where f(x) = { (2x3@3(x1),)┤ 8(x ≤0@x>0)Finding limit at x = 0lim┬(x→0) f(x) = lim

Www3 Nd Edu Apilking Math Work Old exams Exam1f13 Solution Pdf

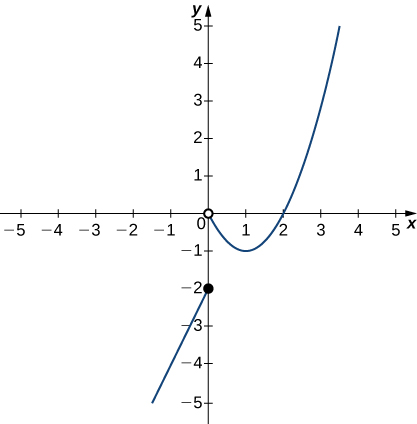
2 2 The Limit Of A Function Calculus Volume 1

Please be sure to answer the questionProvide details and share your research!Thanks for contributing an answer to Mathematics Stack Exchange! Transcript Ex 131, 26 (Method 1) Evaluate lim x 0 f(x), where f(x) = 0, , x 0 x=0 Finding limit at x = 0 lim x 0 f(x) = lim x 0 f(x) = lim x 0 f(x) Thus, lim x 0 f(x) = 1 & lim x 0 f(x) = 1 Since 1 1 So, f(x) f(x) So, left hand limit & right hand limit are not equal Hence, f(x) does not exist Ex131, 26 (Method 2) Evaluate lim x 0 f(x), where f(x) = x x 0, , x 0 x=0 We know that lim x

Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw4solutions Pdf

Limits

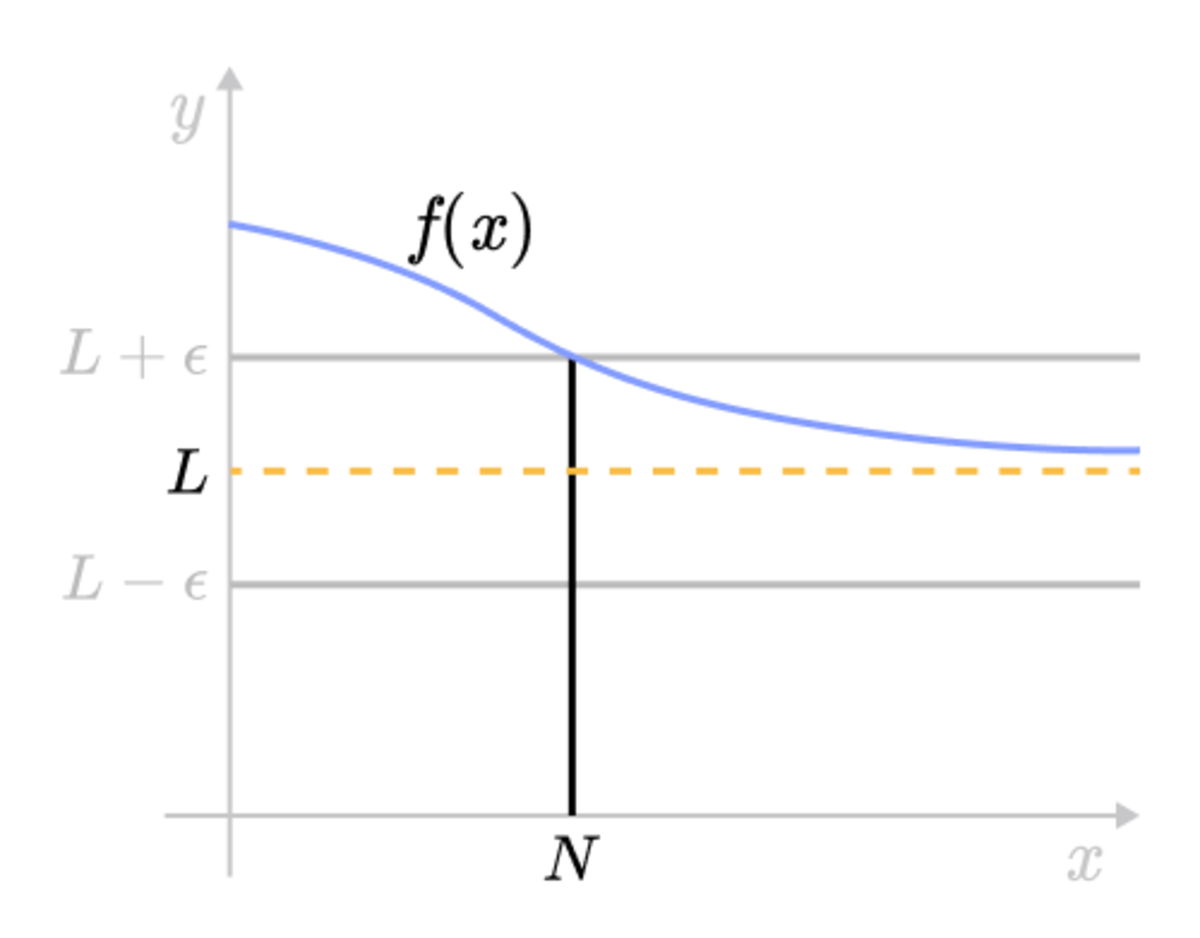
 Explanation lim x→a f (x) = L is and only if for every positive ε, there is a positive δ such that, for all x, if 0 < x −a < δ, then f (x) −L) < ε L cannot be a symbol that does not represent a number The distance between f (x) and L, ( f (x) −L) must be defined∞ 1/0, for example one can write lim x→∞xe −x as lim x→∞x/e xor as lim x→∞e −x/(1/x) To see that the exponent forms are indeterminate note that ln00 = 0ln0 = 0(−∞) = 0 ·∞, ln∞0 = 0ln∞= 0 ·∞, ln1∞= ∞ln1 = ∞·0 = 0 ·∞ These formula's also suggest waysX/23 when x›2 We learn how to evaluate a limit at a given point

1

Limits At Infinity Infinite Limits And Asymptotes

Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learnH = f(g(x 0)∆g)−f(g(x 0)) = f(g ∆g)−f(g) Thus we apply the fundamental lemma of differentiation, h = f0(g)η(∆g)∆g, 1 f0(g)η(∆g) ∆g h Note that f0(g(x)) > 0 for all x ∈ (a,b) and η(∆g) → 0 as h → 0, thus, lim h→0 ∆g/h = lim h→0 1 f0(g)η(∆g) 1 f0(g(x)) Thus g0(x) = 1 f0(g(x)), g 0(f(x)) = 1 f0(x) 3 Suppose g is a real function on R1, with bounded Therefore, we can apply L'Hôpital's rule and obtain lim x → 0 lnx cotx = lim x → 0 1 / x − csc2x = lim x → 0 1 − xcsc2x Now as x → 0 , csc2x → ∞ Therefore, the first term in the denominator is approaching zero and the second term is getting really large In such a case, anything can happen with the product

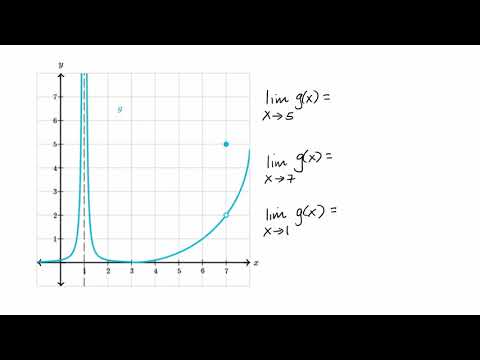
Estimating Limit Values From Graphs Video Khan Academy

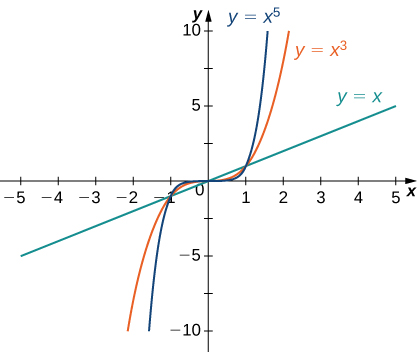
1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts

0, lim x 0 1 x =−∞ , on écrit alors lim x 01 x =−∞ Asymptote verticale Lorsque lim x x0 f x = ∞ ou lim x x0 f x =−∞ , la courbe représentative de f admet la droite d'équation x = x0 comme asymptote verticale 4 Asymptotes obliques Soit f une fonction de courbe C dans le plan muni d'un repèreIndeed, the limit definition of the derivative is the limit of an indeterminate form f ′ ( 0) f' (0) f ′(0)Fig 5 y = ax / x where a = 2 Fig 6 y = x / x 3 The indeterminate form 0 / 0 {\displaystyle 0/0} is particularly common in calculus , because it often arises in the evaluation of derivatives using their definition in terms of limit

Find The Limit If It Exists If The Limit Does Not Chegg Com

Www Ndsu Edu Pubweb Wcasper Hw Solns Hw3 Solns Pdf

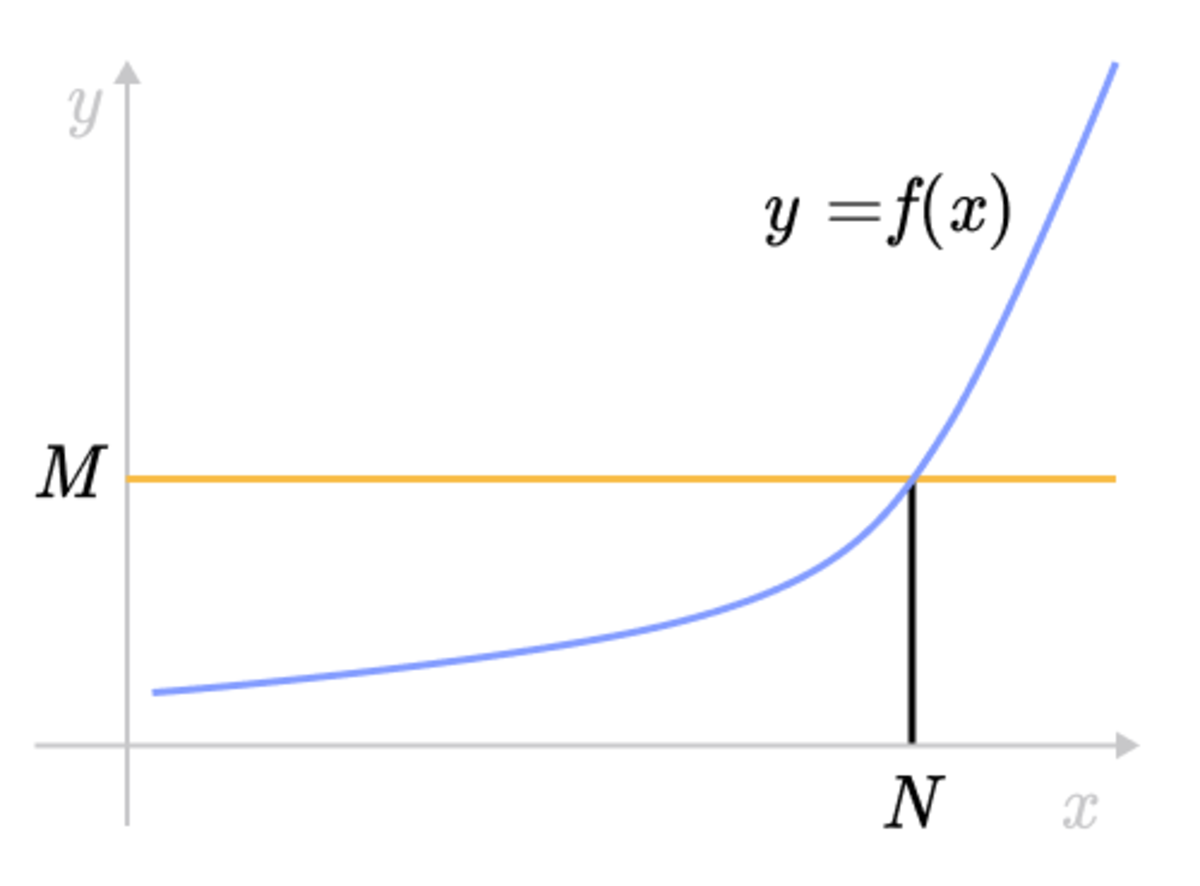
D e f i n i t i o n x → a lim f (x) = ∞ means that for all α > 0, there exists δ > 0 such that if 0 < x − a < δ, then f (x) > α E x a m p l e More Items ShareThe relationship of limit inferior and limit superior for sequences of real numbers is as follows → = → As mentioned earlier, it is convenient to extend to −∞,∞ Then, (x n) in −∞,∞ converges if and only if→ = → in which case → is equal to their common value (Note that when working just in , convergence to −∞ or ∞ would not be considered as convergence) Set f (x) = x1 x then take logarithms on both sides lnf (x) = 1 x ⋅ lnx f (x) = elnx x Now we must find the limit lim x→0 lnx x We observe that this is lim x→0 lnx x = −∞ 0 which is actually "equal" to negative infinity

Prove Lim As X Approaches To 1 F X Infinite Mathematics Stack Exchange

Solution Evaluate Lim X 3x 4 2x 2 7 5x 3 X 3

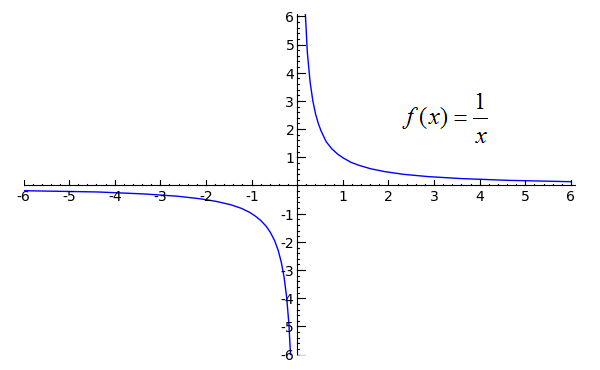
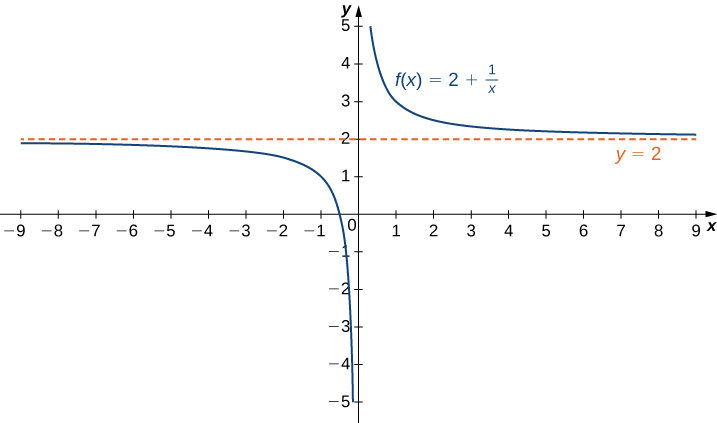
For example, for the function f (x) = 1 x, f (x) = 1 x, since lim x → ∞ f (x) = 0, lim x → ∞ f (x) = 0, the line y = 0 y = 0 is a horizontal asymptote of f (x) = 1 x f (x) = 1 x1 = lim b→∞ − ln(b) b −01 L'H= lim b→∞ − 1/b 1 1 = 01 = 1 L'Hôpital's Rule Suppose that f(a) = g(a) = 0, that f(x) and g(x) are differentiable on an open interval I containing a and that g′(x) 6= 0 on I if x 6= a Then lim x→a f(x) g(x) = lim x→a f′(x) g′(x), assuming thatSolution for 3 What is lim f(x)?

Finding Limits Graphically

Calculus I Limits At Infinity Part I

Evaluate limit as x approaches 6 of F(x) Move the term outside of the limit because it is constant with respect to Evaluate the limit of by plugging in for

Ex 13 1 23 Find Lim X 0 And Lim X 1 Where F X 2x 3 3 X 1

Lim X Tends To 0 1 X 1 X E X Is Equal To Brainly In

Limits

Web Auburn Edu Holmerr 1617 Textbook Limatinfty Print Pdf

What Is The Limit As X Approaches Infinity Of X 2 4 2x 4x 2 Socratic

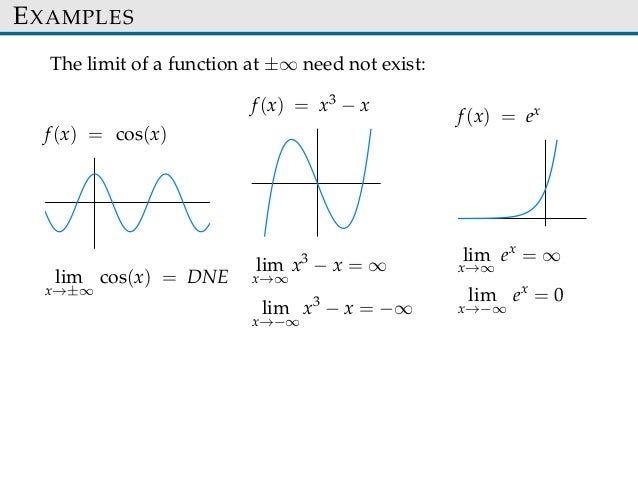
Limits Involving Infinity Ppt Download

Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki

Ex 13 1 25 Find Lim X 0 Where F X X X 0 Teachoo

Given That Lim X Rightarrow A F X 0 Lim X Chegg Com

Faculty Math Illinois Edu Lfolwa2 Gw Sol Pdf

Limits To Infinity

Show That Lim X 0 1 X Does Not Exist

Left Hand And Right Hand Limits What Is Left Hand And Right Hand Limits Examples Solutions Cuemath

Ex 13 1 27 Find Lim X 5 F X Where F X X 5 Teachoo

Limite Functions Sect22 24

How Can E X Seemingly Approach 0 As X Approaches Negative Infinity Mathematics Stack Exchange

Finding Limits Graphically

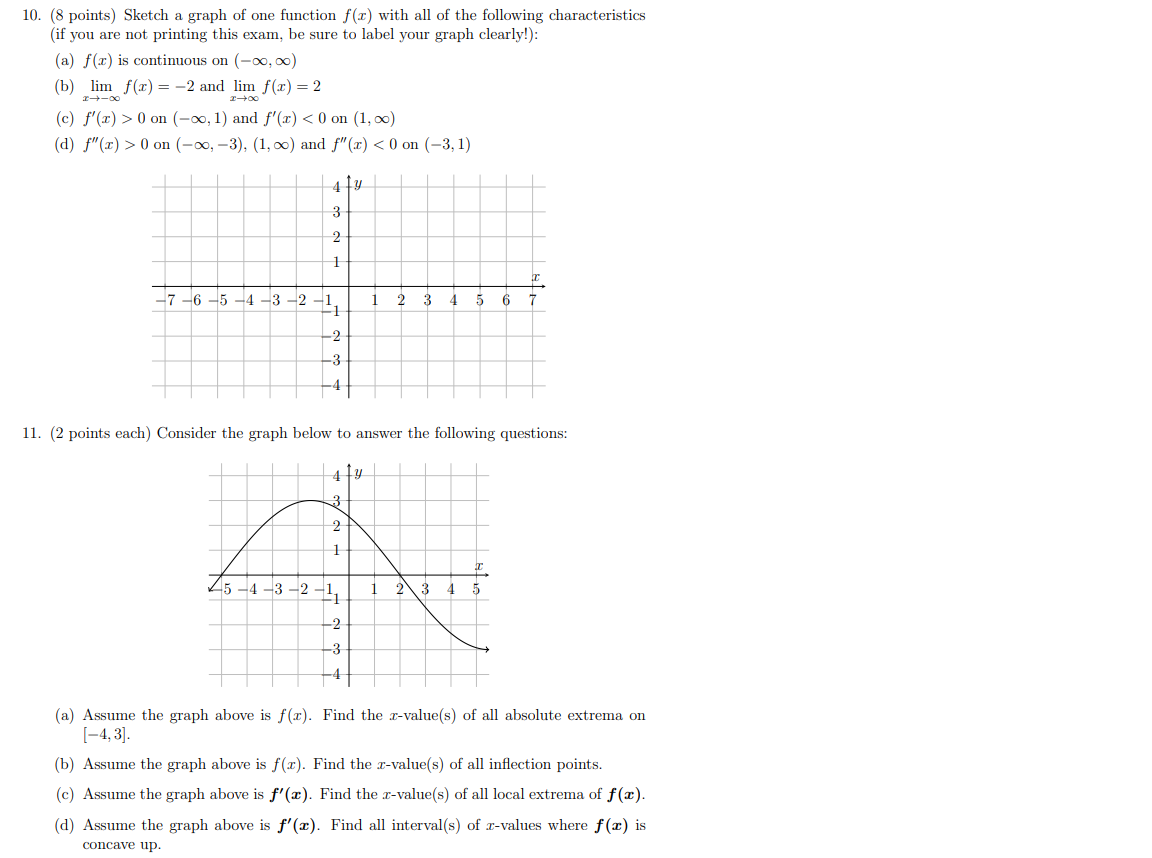
10 Sketch A Graph Of One Function F X With All Of Chegg Com

X 1 1 X 1 31 X 2 3 Maths Questions

Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki

1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts

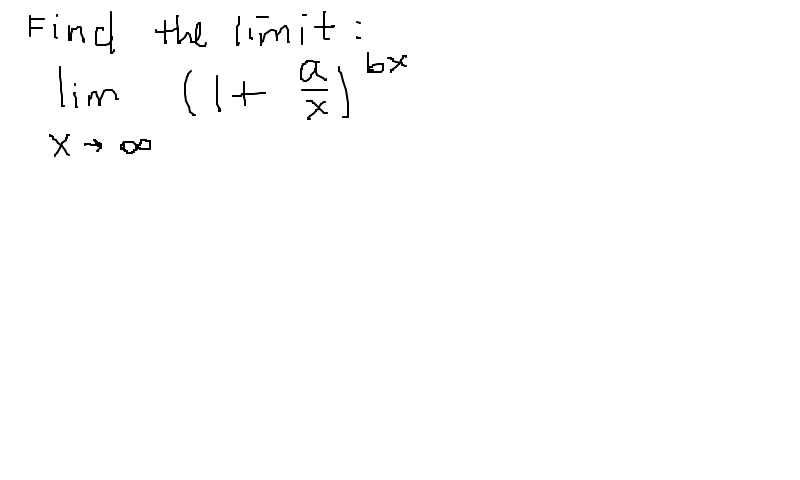
What Is The Limit As X Approaches Infinity Of 1 A X Bx Socratic

2 2 The Limit Of A Function Calculus Volume 1

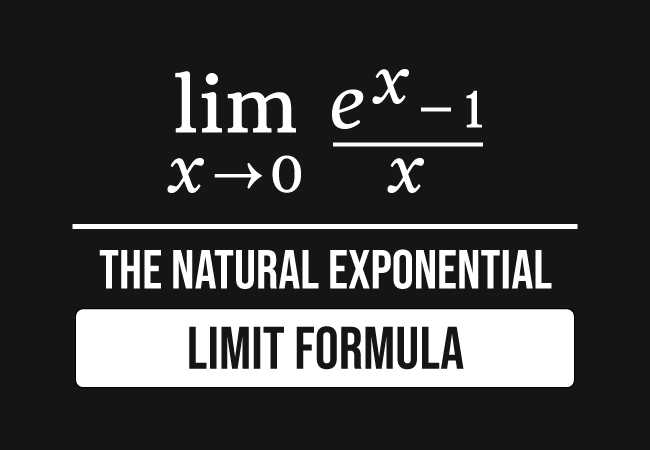
Lim X 0 E X 1 X Formula

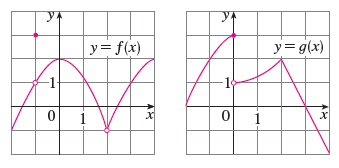
Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant

Limits At Infinity Concept How To Solve With Examples

Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora

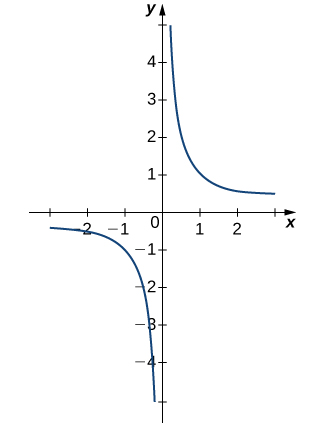
2 2 The Limit Of A Function Calculus Volume 1

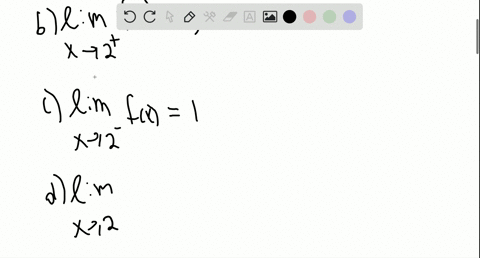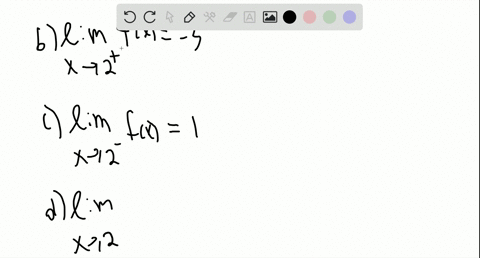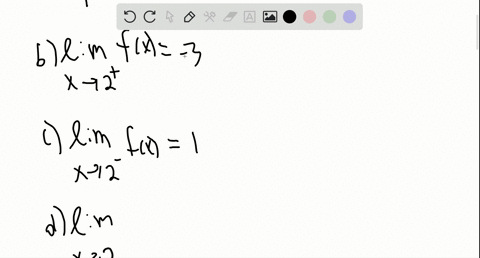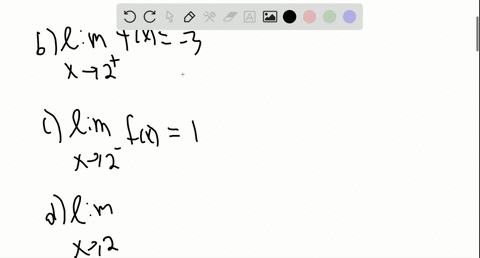
Solved A For F X Frac X Ln X Find Each Of The Following Limits I Displaystyle Lim X To 0 F X Ii

Evaluate The Limit Limx 5x 3 6 9 4x 6 Sarthaks Econnect Largest Online Education Community

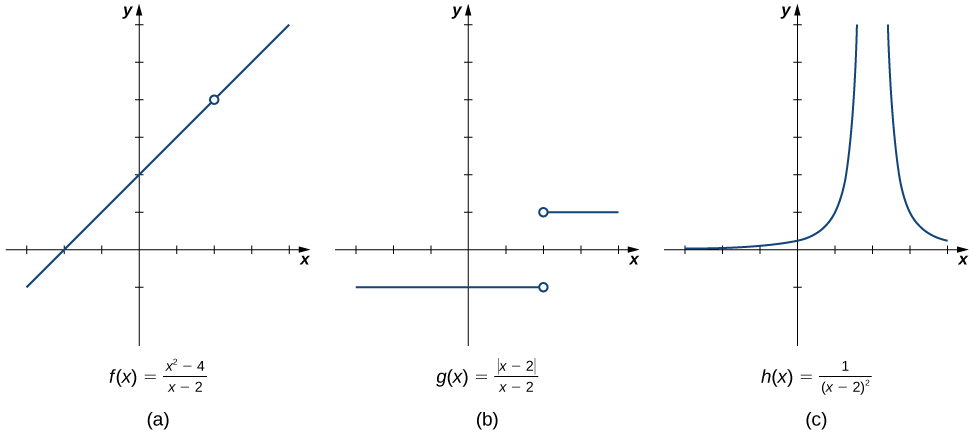
2 2 The Limit Of A Function Calculus Volume 1

Prove That Lim X To Infty Frac 1 X Int 0 Xf T Dt A If F Is Continuous And Lim X To Infty F X A Mathematics Stack Exchange

Limits At Infinity Of Quotients Part 1 Video Khan Academy

Limit Of A Function Wikipedia

Limits

Users Math Msu Edu Users Zhan Hw13 Solution Pdf

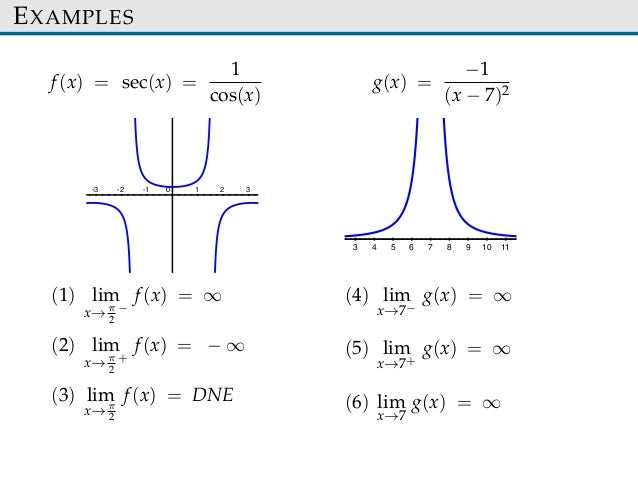
Limite Functions Sect22 24

Limit Of 1 2x 1 X As X Goes To 0 L Hospital S Rule Youtube

Limits 2 Continuous Function Compact Space

Www Southalabama Edu Mathstat Personal Pages Jbarnard Archive Teaching Sm13 125 Test1sol Pdf

Ex 13 1 31 If Function F X Lim X 1 F X 2 X2 1 Pi

A Function F Is Even If F X F X For All X In The Chegg Com

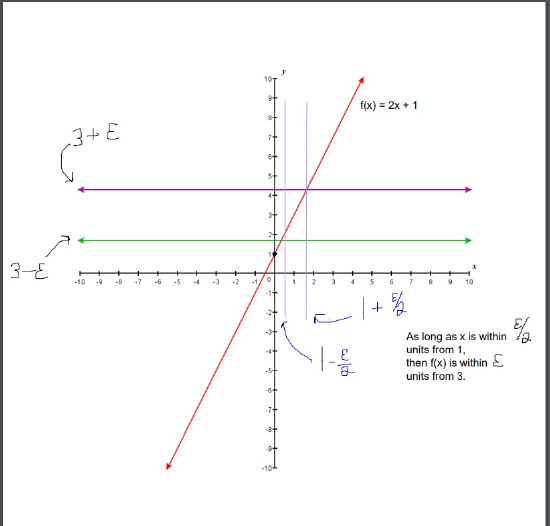
2 7 The Precise Definition Of A Limit Mathematics Libretexts

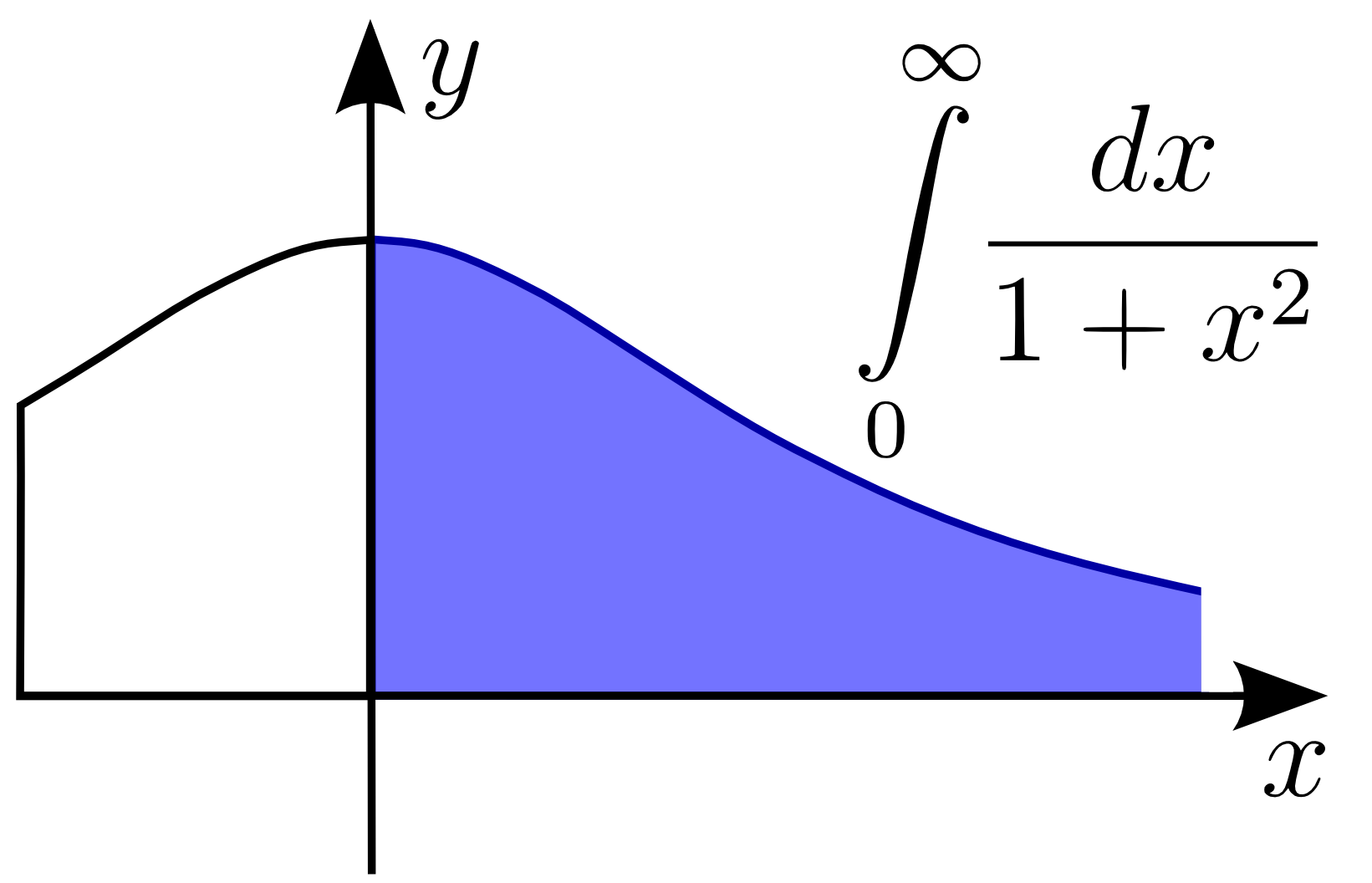
Improper Integral Wikipedia

Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora

For The Function F Whose Graph Is Given State The Chegg Com

7 F X Lim

Limits At Infinity Concept How To Solve With Examples

Use The Formula F X Lim X A F X F A X A Mathskey Com

Www Alamo Edu Contentassets 691fef0cb473b980bb6648fb Functions Math1325 1 Sided Limits Pdf

Lim X 1 X 2 X Lnx Lnx 1 X 1

Www Ndsu Edu Pubweb Wcasper Hw Solns Hw3 Solns Pdf

Answered Lim F X 0 Lim G X 0 Lim H X 1 Bartleby

Solved A For F X Frac X Ln X Find Each Of The Following Limits I Displaystyle Lim X To 0 F X Ii

Limit Calculator Wolfram Alpha

1

Calculus Limits

How To Determine If A Limit Does Not Exist Video Lesson Transcript Study Com

Calculus Limits

Www Math Ucla Edu Archristian Teaching 31a W16 Week 2 Pdf

Theorem For Limits Of Composite Functions Video Khan Academy

Www3 Nd Edu Apilking Math Calc1lectures Lecture 3 limits Pdf

Web Auburn Edu Holmerr 1617 Textbook Lhopital Print Pdf

Indeterminate Forms

Solution Evaluate Lim X 3x 4 2x 2

Web Stanford Edu Class Archive Math Math41 Math41 1142 Oldexams 12exam1sol Pdf

What Is The Limit Of 1 X As X Approaches 0 Quora

Q Tbn And9gcts 9crf6alsdqc Qry4glqrpijax Xo9biizzm6szydtzopk1l Usqp Cau

Calculus Limits At Infinity The Limit Of X Sqrt X 2 X As X Approaches Negative Infinity Youtube

2 5 Continuity A Continuous Function Is One That Can Be Plotted Without The Plot Being Broken Is The Graph Of F X A Continuous Function On The Interval Ppt Download

Finding The Limit Free Math Help

Limit As X Approaches Negative Infinity For X 2 2x 3 1 2 X Youtube